1. Tanım

• Pusula ve harita kullanılarak bilinmeyen bir konumun belirlenmesini sağlayan açı tabanlı navigasyon yöntemi.
• Üçgenleme prensibi ile iki veya daha fazla noktadan ölçülen açıların kesişiminden pozisyon hesaplanır.

2. Amaç

• Harita üzerinde mevcut konumu tespit etmek.
• Doğada, denizde veya askeri operasyonlarda yön bulma ve rota planlama.

3. Gerekli Araçlar

• Pusula (açı ölçümü için).
• Detaylı harita (nirengi noktaları ve topografik bilgiler içeren).
• Kalem/cetvel (çizim yapmak için).
• Manyetik sapma (deklinasyon) değeri (bölgeye özgü).

4. Adımlar

a. Nirengi Noktalarının Seçimi

• Harita ve arazide  belirgin, kolay tanımlanabilir iki veya üç nokta seçilir (örneğin: tepe, yapı, kule, göl).

b. Kerteriz Ölçümü

• Pusula yatay tutularak nirengi noktalarına olan manyetik açılar ölçülür.
• Örnek: İlk nokta için 45°, ikinci nokta için 120° okunması.

c. Manyetik Sapma Düzeltmesi

• Manyetik kuzey ile gerçek kuzey arasındaki deklinasyon değeri eklenir.
• Örnek: Türkiye’de ortalama ~6° Doğu sapması vardır, 45° + 6° = 51° gerçek açı. (Sapma açısının güncelliğini kontrol edin)

d. Geri Kerteriz Hesaplama

Geri Dönüş Kerterizi Nedir?

Geri dönüş kerterizi, belirli bir noktadan ölçülen açının ters yönünü ifade eder.

• Ölçülen açıya 180° eklenerek geri kerteriz bulunur. (Açımız 180 den büyük ise 180 çıkarırız 180 den küçük ise 180 ekleriz)
• Örnek: 51° → 51° + 180° = 231°.

e. Harita Üzerinde Çizim

• Her noktadan geri kerteriz yönünde düz çizgiler çizilir.
• Örnek: İlk noktadan 231°, ikinci noktadan 300° yönünde çizgiler.

f. Kesişim Noktasının Belirlenmesi

• Çizgilerin kesiştiği nokta mevcut konumu gösterir.
• Üç nokta kullanılırsa, hata üçgeni oluşabilir; konum bu üçgen içindedir.

5. Hata Kaynakları

• Manyetik hatalar: Metal objeler, elektrik hatları pusulayı saptırır.
• Yanlış deklinasyon düzeltmesi.
• Nirengi noktalarının yanlış tanımlanması.
• Çizim hataları (ölçeksiz veya eğri çizgiler).

6. Uygulama Alanları

• Doğa sporları
• Askeri operasyonlar
• Arama-kurtarma çalışmaları.
• Denizcilik ve havacılık navigasyonu.

7. Önemli İpuçları

• Açı ölçümünde pusula düz ve sabit tutulmalı.
• Harita ile pusulanın kuzeyi aynı hizaya getirilmeli. (Tercihen)
• Mümkünse üç nokta kullanılarak hata payı azaltılmalı.

Sonuç: Pusula üçgenleme, temel navigasyon becerilerinden biridir ve doğru uygulandığında yüksek hassasiyet sağlar. Pratik yaparak hata kaynakları minimize edilebilir.

NOTLAR

Türkiye’de manyetik sapma açısı (pusula sapma açısı), manyetik kuzey ile coğrafi (gerçek) kuzey arasındaki açısal farktır. Bu değer konuma ve zamana göre değişir. Bu değerler yıllık olarak artı/eksi 0.1°-0.2° değişir.

1. Haritadan Pusulaya Açı Hesaplama (Gerçek Kuzey → Manyetik Kuzey)

Haritada ölçtüğünüz gerçek açıyı, pusula ile kullanmak için **manyetik sapma açısını çıkarırsınız**.

Formül:
Pusula Açısı = Harita Açısı − Doğu Sapması

Örnek:
Haritada bir noktaya 100° (gerçek kuzeye göre) yönünüz var. Sapma açısı 6° Doğu ise: 
`100° − 6° = 94°` 
Pusulanızı  94° ye ayarlayarak ilerlersiniz.

—

2. Pusuladan Haritaya Açı Hesaplama (Manyetik Kuzey → Gerçek Kuzey)

Pusuladan okuduğunuz açıyı haritaya işlemek için **manyetik sapma açısını eklersiniz**.

Formül:
Harita Açısı = Pusula Açısı + Doğu Sapması

Örnek:
Pusulanız 80° gösteriyor (manyetik kuzeye göre). Sapma açısı 6° Doğu ise: 
`80° + 6° = 86°` 

Haritada bu yönü 86°  olarak işaretlersiniz.

Özet Tablo

Örnek (Sapma: 6° Doğu)

Harita → Pusula   =     Çıkarma (Gerçek − Sapma) | 100° → **94°**     

Pusula → Harita  =   Toplama (Manyetik + Sapma) | 95° → **101°** 

Sapma açısı dikkate alınmazsa, özellikle uzun mesafelerde hedef şaşma riski oluşur. Doğru navigasyon için bu düzeltmeyi yapmak kritiktir.

Pusula Üçgenlemede İki Nirengi Noktası Arasındaki Açı Farkı Ne Kadar Olmalı?

Pusula üçgenlemede, iki nirengi noktasından ölçülen açıların kesişim hassasiyeti için ideal açı farkı 60° ile 120° arasında olmalıdır. Bu aralık, konumun doğru ve net belirlenmesini sağlar. İşte detaylar:

1. İdeal Açı Farkı Neden Önemli?

• Dar Açılar (0°-60°):
• Kesişim çizgileri birbirine çok yakın olur.
• Hata payı artar, konum belirsizleşir.
• Örnek: 20° ve 40° açı farkı → Kesişim bulanık.
• Geniş Açılar (120°-180°):
• Kesişim çizgileri çok uzaklaşır.
• Hassasiyet azalır, konum geniş bir alana yayılır.
• Örnek: 150° ve 170° açı farkı → Kesişim belirsiz.
• En Uygun Aralık (60°-120°):
• Kesişim çizgileri net ve keskin olur.
• Örnek: 50° ve 110° → Kesişim noktası belirgin.

2. Pratik Öneriler

• Nirengi noktalarını seçerken:
• Birbiriyle yaklaşık 90° açı yapacak iki nokta tercih edin.
• Örnek: Biri kuzeydoğuda (45°), diğeri güneybatıda (225°) olan iki tepe.
• Üç nokta kullanın:
• İki nokta yetersiz kalırsa, üçüncü bir nokta ekleyerek “hata üçgeni”ni küçültün.

3. Hesaplama ve Uygulama

• Adım 1: İki noktadan açıları ölçün (örneğin, 80° ve 140°).
• Adım 2: Açı farkını hesaplayın: 140° – 80° = 60° (ideal aralıkta).
• Adım 3: Haritaya geri kerteriz çizgilerini çizerek kesişim noktasını bulun.

4. Dikkat Edilmesi Gerekenler

• Manyetik sapma düzeltmesi yapın: Türkiye’de ~6° Doğu sapmasını ekleyin.
• Nirengi noktaları net olmalı: Belirgin tepeler, kuleler veya yapılar seçin.
• Pusulayı yatay tutun: Eğim, ölçüm hatasına yol açar.

5. Örnek Senaryo

• Nokta A: Bir dağ zirvesi (kerteriz: 50°).
• Nokta B: Bir radyo kulesi (kerteriz: 120°).
• Açı Farkı: 120° – 50° = 70° (ideal aralıkta).
• Sonuç: İki çizginin kesiştiği nokta, konumunuzu hassas şekilde gösterir.

---

Sonuç:

İki nirengi noktası arasındaki açı farkı 60°-120° arasında olursa, pusula üçgenleme ile en doğru sonucu alırsınız. Pratikte 90° açı farkı hedefleyin ve üç nokta kullanarak hata payını azaltın.

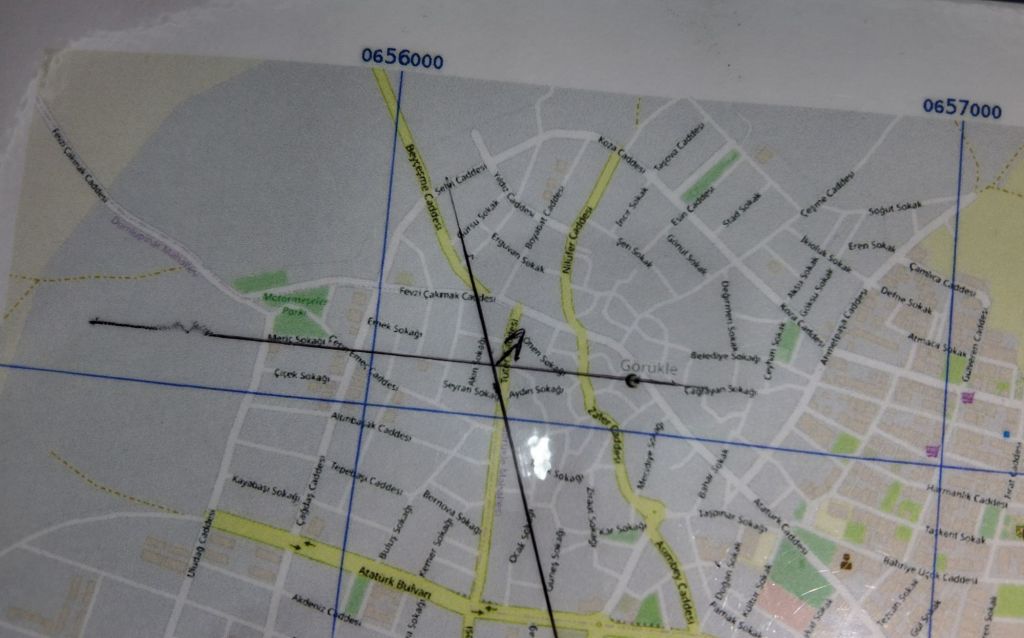
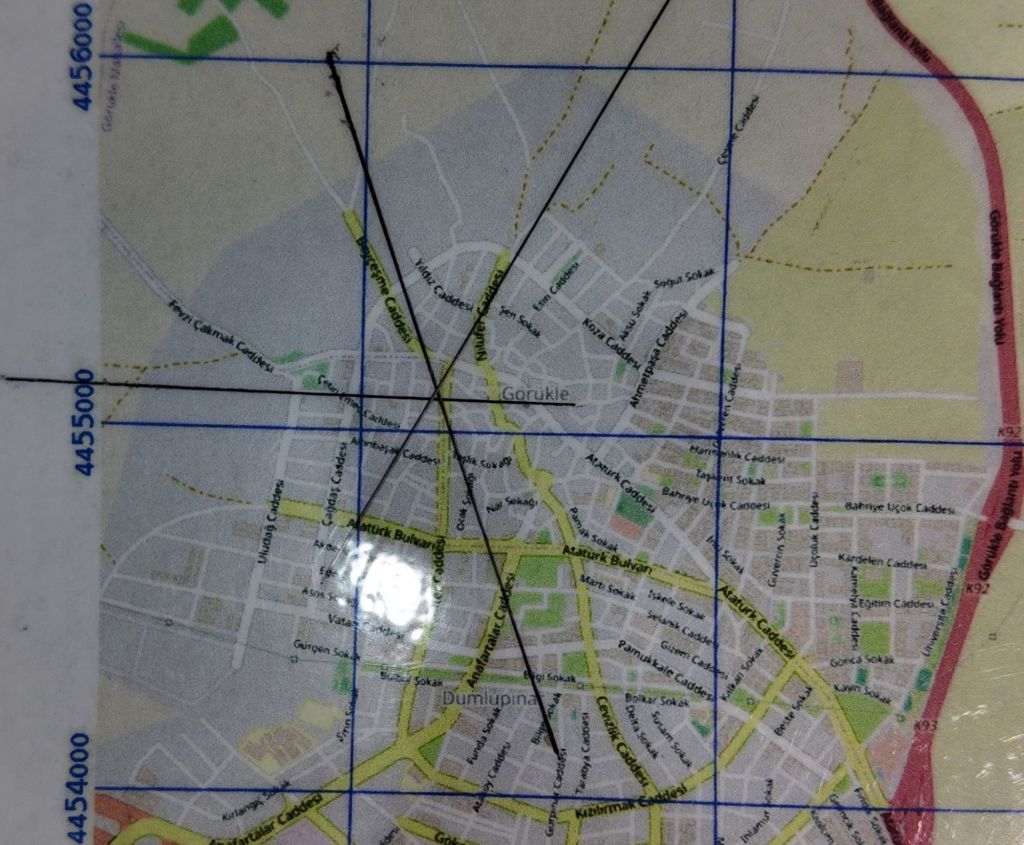
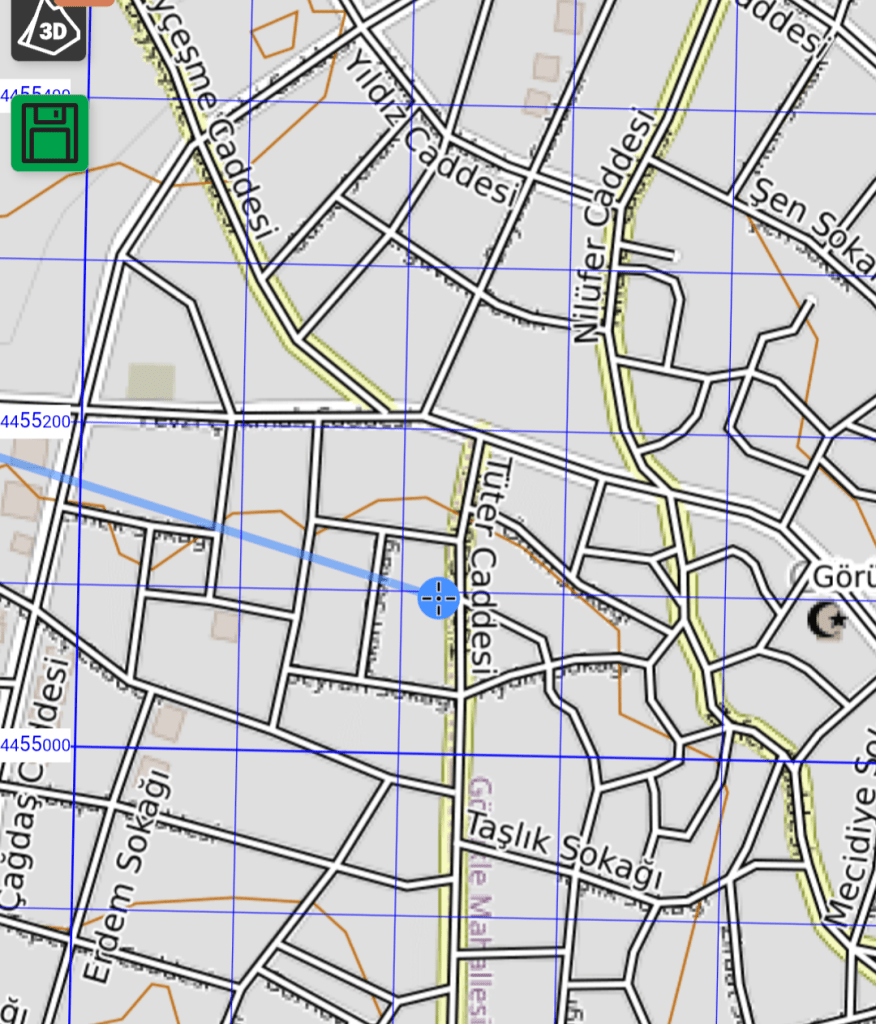
ÇALIŞMA FOTOĞRAFLARI VE VİDEO